supplykasce.blogg.se - Simple famous determinate finite state automata

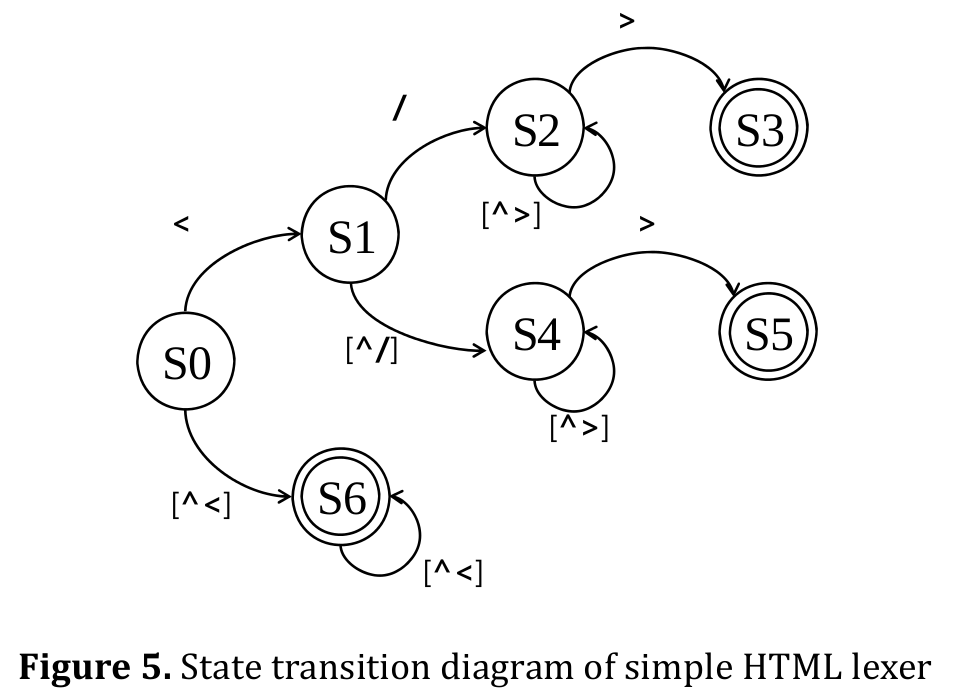
This method achieves greater generality than previous methods because building the backward depth information is independent of the topological complexity of the DFA.

Few states need to be refined by the hash table, because most states have been partitioned by the backward depth information in the coarse partition. The minimization algorithm has a lower time complexity O( n) than a naive comparison of transitions O( n 2). In the second phase, the state set is refined using a hash table. In the first phase, the backward depth information is built, and the state set of the DFA is partitioned into many blocks. A minimization algorithm is presented in this paper that consists of two main phases. From the DFA, the acceptable strings can be derived.Obtaining a minimal automaton is a fundamental issue in the theory and practical implementation of deterministic finite automatons (DFAs). Let us consider the DFA shown in Figure 1.3. The language L′ not accepted by DFA/NDFA (Complement of accepted language L) is Moore Machine − The output depends only on the current state.Ī string is accepted by a DFA/NDFA iff the DFA/NDFA starting at the initial state ends in an accepting state (any of the final states) after reading the string wholly.Ī string S is accepted by a DFA/NDFA (Q, ∑, δ, q 0, F), iffĪ string S′ is not accepted by a DFA/NDFA (Q, ∑, δ, q 0, F), iff Mealy Machine − The output depends both on the current state and the current input. TransducerĪn automaton that produces outputs based on current input and/or previous state is called a transducer. ClassifierĪ classifier has more than two final states and it gives a single output when it terminates. All the states of an acceptor is either accepting or rejecting the inputs given to it. In NDFA, backtracking is not always possible.Ī string is accepted by a DFA, if it transits to a final state.Ī string is accepted by a NDFA, if at least one of all possible transitions ends in a final state.Īcceptors, Classifiers, and Transducers Acceptor (Recognizer)Īn automaton that computes a Boolean function is called an acceptor. Hence it is called non-deterministic.Įmpty string transitions are not seen in DFA. The transition from a state can be to multiple next states for each input symbol. The transition from a state is to a single particular next state for each input symbol. The following table lists the differences between DFA and NDFA. Its graphical representation would be as follows − DFA vs NDFA The transition function δ as shown below − Present State

Let a non-deterministic finite automaton be →

The final state is indicated by double circles.

The initial state is denoted by an empty single incoming arc.

The arcs labeled with an input alphabet show the transitions.

Graphical Representation of an NDFA: (same as DFA)Īn NDFA is represented by digraphs called state diagram. Q 0 is the initial state from where any input is processed (q 0 ∈ Q).į is a set of final state/states of Q (F ⊆ Q). (Here the power set of Q (2 Q) has been taken because in case of NDFA, from a state, transition can occur to any combination of Q states) Δ is the transition function where δ: Q × ∑ → 2 Q ∑ is a finite set of symbols called the alphabets. Formal Definition of an NDFAĪn NDFA can be represented by a 5-tuple (Q, ∑, δ, q 0, F) where − As it has finite number of states, the machine is called Non-deterministic Finite Machine or Non-deterministic Finite Automaton. Hence, it is called Non-deterministic Automaton. In other words, the exact state to which the machine moves cannot be determined. In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine.